Cosmology Paradoxes
The word paradox is derived from the Greek prefix para-, meaning ‘contrary or opposed’, and the word doxos, meaning ‘opinion’. As defined by the Oxford English Dictionary, paradox is ‘a statement or tenet contrary to received opinion or belief, especially one that is difficult to believe’. Theoretical physicist Richard Feynman once said,
The ‘paradox’ is only a conflict between reality and your feeling of what reality ‘ought to be’.
In this piece, I have tried to explain five great paradoxes to ever exist in cosmology and astrophysical sciences.
Bentley’s Paradox
In 1692, five years after the first publication of Principia, Rev. Richard Bentley wrote a dis-alarmingly simple yet distressing letter to Newton. He asked a simple question that even Newton had no answer. Since gravity was always attractive and never repulsive, this meant that any collection of stars would naturally collapse into themselves. If the universe was finite, then the night sky instead of being eternal and static, the stars should plow into each other and coalesce into a fiery superstar. But he also pointed out that if the universe were infinite, then the force on any object, tugging it to the left or right, would also be infinite, and therefore the stars should be ripped to shreds in fiery cataclysms.
Either possibility the universe was finite or infinite was a disaster for the young theory. This Problem for the first time in history, revealed the subtle but inherent paradoxes that riddle any theory of gravity when applied to the entire universe.


Newton’s Response:
In his response to Bentley, Newton wrote that he would prefer an infinite universe but one that was totally uniform. A star that experiences an infinite force from the left also experiences the same amount of force from the right. The forces nullify each other leading to a stable stellar system.
According to Newton, the universe was like a gigantic clock wound at the beginning of time by God, which has been ticking away ever since, according to the laws of motion, without Divine interference. But at times, even God himself had to intervene and tweak the universe a bit to prevent it from collapsing.
Hence Newton’s answer was “God” and he solved Bentley’s paradox by claiming that God prevented the collapse by making constant interventions and corrections.
Heat Death Paradox
In 1862 Lord Kelvin, Hermann von Helmholtz and William John Macquorn Rankine, formulated the heat death paradox, also known as Clausius’s paradox and thermodynamic paradox. It is a reductio ad absurdum argument that uses thermodynamics to show the impossibility of an infinitely old universe.
Assuming that the universe is eternal, a question arises: How is it that thermodynamic equilibrium has not already been achieved?
This paradox is based upon the classical model of the universe in which the universe is eternal. Clausius’s paradox is a paradox of paradigm. It was necessary to amend the fundamental ideas about the universe, which brought about the change of the paradigm. The paradox was solved when the paradigm was changed.
There are at least two common resolutions to this. First is that it doesn’t apply to a universe in a steady state where there is a continual destruction and recreation of energy and matter, a theory popular in the early/mid twentieth century and, more pertinently with our current state of knowledge, to a universe which does appear to have a starting point in the form of the “Big Bang”.
There are many other cosmological theories around which even provide a variation on continuous recreation, but none of them suffer from the “heat death paradox” as none are closed systems in the manner required for classical thermodynamics to apply.



Fermi Paradox
The Fermi Paradox is a conjecture made by physicist Enrico Fermi, allegedly over lunch with Edward Teller, amongst others, at Los Alamos in 1950 where they were having a casual lunchtime conversation about the abundance of stars and the likelihood that given the amount of stars, there ought to be lots of alien civilizations out there. The conversation then mutated to other topics, as lunch conversations tend to do and nobody thought about it — until Fermi suddenly burst out “Where are they?” The idea is that if technology using life existed elsewhere in the galaxy, the odds are it would have visited by now, given the age of the galaxy and the relatively trivial amount of time it would take a civilization only moderately more advanced than ours to colonize the galaxy.


There are billions of stars in the galaxy that are similar to our Sun
Many of which are as old or older than our Sun
Many of these Stars having Earth-like planets
Some of which would have have had more time, even billions of years to develop intelligent life
Some of whom might develop interstellar travel (or some method of communicating with us)
Even at the slow pace of currently envisioned interstellar travel, the Milky Way galaxy could be completely traversed in a few million years
But why haven’t we found an alien life yet? Why haven’t they visited us? This is the basis of the Fermi paradox: despite there being so many stars out there with so many planets that could conceivably have their own civilizations, why haven’t we heard from them?
Drake’s Equation
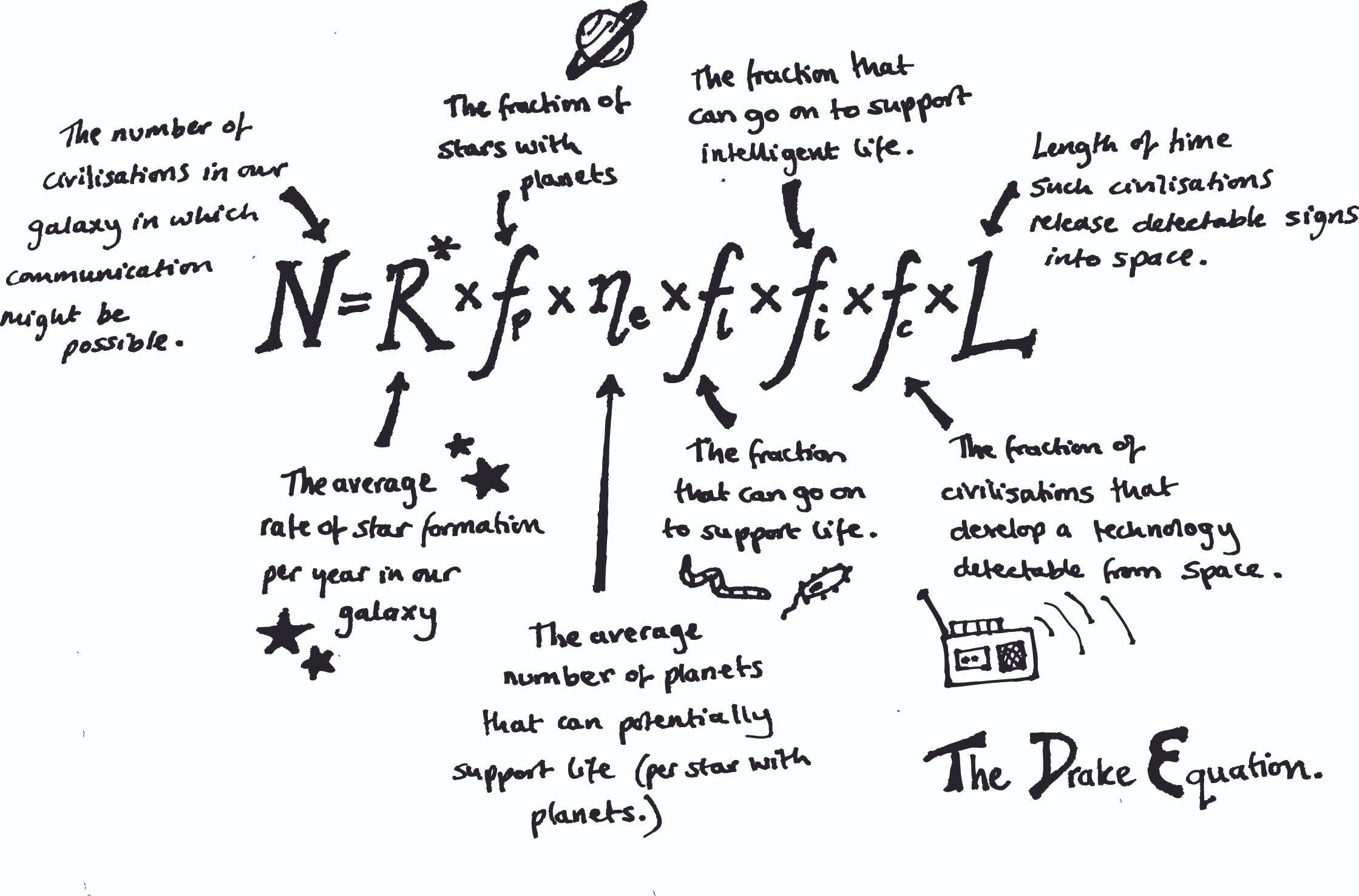
The Drake Equation is used to estimate the number of communicating civilizations in our galaxy, or more simply put, the odds of finding intelligent life in the Milky Way. First proposed by astronomer Frank Drake in 1961, the equation calculates the number of communicating civilizations by multiplying several variables:
N = The number of civilizations in the Milky Way galaxy whose electromagnetic emissions are detectable.
R* = The rate of formation of stars suitable for the development of intelligent life.
fp = The fraction of those stars with planetary systems.
ne = The number of planets, per solar system, with an environment suitable for life.
fl = The fraction of suitable planets on which life actually appears.
fi = The fraction of life bearing planets on which intelligent life emerges.
fc = The fraction of civilizations that develop a technology that releases detectable signs of their existence into space.
L = The length of time such civilizations release detectable signals into space.
Boltzmann brain
In the physical universe at large, the second law of thermodynamics says that entropy must increase over time — that is, everything will become less orderly. It’s possible, though, for certain areas of the universe to become slightly more orderly as the result of random fluctuations, as long as other parts of the universe become less orderly at the same time. We live in an incredibly orderly part of the universe. Just a short strand of DNA is so intricately constructed that the probability of it arising as a result of “random fluctuations” in physical material is unthinkably small. So how is it that there are billions of base pairs in a single cell, trillions of cells in a complex organism, and millions of species on Earth?
Boltzmann brain is a thought experiment. In this thought experiment, a Boltzmann brain is a fully formed brain, complete with memories of a full human life in our universe, that arises due to extremely rare random fluctuations out of a state of thermodynamic equilibrium. Theoretically, over an extremely large but not infinite amount of time, by sheer chance, atoms in a void could spontaneously come together in such a way as to assemble a functioning human brain. Like any brain in such circumstances (the hostile vacuum of space with no blood supply or body), it would almost immediately stop functioning and begin to deteriorate.

The idea is named after the Austrian physicist Ludwig Boltzmann (1844–1906), who, in 1896, published a theory that tried to account for the fact that humans find themselves in a universe that is not as chaotic as the budding field of thermodynamics seemed to predict.
Ludwig Boltzmann reasoned that brains and other complex, orderly objects on Earth were the result of random fluctuations. But why do we see billions of other complex, orderly objects all around us? Boltzmann theorized that if random fluctuations create brains like ours, there should be Boltzmann brains floating around in space or sitting alone on uninhabited planets untold lightyears away. And in fact, those Boltzmann brains should be incredibly more common than the herds of complex, orderly objects we see here on Earth.
The Boltzmann Brain paradox is an argument against the idea that the universe around us, with its incredibly low-entropy early conditions and consequential arrow of time, is simply a statistical fluctuation within some eternal system that spends most of its time in thermal equilibrium.
The first invocation of an argument along these lines came from Sir Arthur Eddington in 1931. But it’s a fairly straightforward argument, once you grant the assumptions (although there remain critics). So I’m sure that any number of people have thought along similar lines, without making a big deal about it.


Richard Feynman, at the end of his chapter on entropy, in the Feynman Lectures on Physics, ponders how to get an arrow of time in a universe governed by time-symmetric underlying laws.
So far as we know, all the fundamental laws of physics, such as Newton’s equations, are reversible. Then were does irreversibility come from? It comes from order going to disorder, but we do not understand this until we know the origin of the order. Why is it that the situations we find ourselves in every day are always out of equilibrium? One possible explanation is the following. Look again at our box of mixed white and black molecules. Now it is possible, if we wait long enough, by sheer, grossly improbable, but possible, accident, that the distribution of molecules gets to be mostly white on one side and mostly black on the other. After that, as time goes on and accidents continue, they get more mixed up again.
Thus one possible explanation of the high degree of order in the present-day world is that it is just a question of luck. Perhaps our universe happened to have had a fluctuation of some kind in the past, in which things got somewhat separated, and now they are running back together again. This kind of theory is not unsymmetrical, because we can ask what the separated gas looks like either a little in the future or a little in the past. In either case, we see a grey smear at the interface, because the molecules are mixing again. No matter which way we run time, the gas mixes. So this theory would say the irreversibility is just one of the accidents of life.
We would like to argue that this is not the case. Suppose we do not look at the whole box at once, but only at a piece of the box. Then, at a certain moment, suppose we discover a certain amount of order. In this little piece, white and black are separate. What should we deduce about the condition in places where we have not yet looked? If we really believe that the order arose from complete disorder by a fluctuation, we must surely take the most likely fluctuation which could produce it, and the most likely condition is not that the rest of it has also become disentangled! Therefore, from the hypothesis that the world is a fluctuation, all of the predictions are that if we look at a part of the world we have never seen before, we will find it mixed up, and not like the piece we just looked at. If our order were due to a fluctuation, we would not expect order anywhere but where we have just noticed it.
After pointing out that we do, in fact, see order (low entropy) in new places all the time, Feynman goes on to emphasize the cosmological origin of the Second Law and the arrow of time:
We therefore conclude that the universe is not a fluctuation, and that the order is a memory of conditions when things started. This is not to say that we understand the logic of it. For some reason, the universe at one time had a very low entropy for its energy content, and since then the entropy has increased. So that is the way toward the future. That is the origin of all irreversibility, that is what makes the processes of growth and decay, that makes us remember the past and not the future, remember the things which are closer to that moment in history of the universe when the order was higher than now, and why we are not able to remember things where the disorder is higher than now, which we call the future.
And he closes by noting that our understanding of the early universe will have to improve before we can answer these questions.
This one-wayness is interrelated with the fact that the ratchet [a model irreversible system discussed earlier in the chapter] is part of the universe. It is part of the universe not only in the sense that it obeys the physical laws of the universe, but its one-way behavior is tied to the one-way behavior of the entire universe. It cannot be completely understood until the mystery of the beginnings of the history of the universe are reduced still further from speculation to scientific understanding.
Black hole information paradox
Law of conservation of information is a core of quantum mechanics. Arguably, it has same importance as superposition principle. Information in terms of quantum mechanics is just a “state” situated within a quantum system (wave-function). Information cannot be created nor destroyed it means a quantum particle can be converted into energy during nuclear fission or fusion but the precious information of the particle situated in its wavefunction cannot be destroyed.
But when a particle falls in event horizon of black hole it is thought that the particle along with its information is lost, since black hole breaks Time reversal symmetry and is supported by No -hair theorem. When Stephen Hawking proposed his equations on thermodynamic radiation from black-holes, it seemed that, information that was initially present in the particles constituting the radiation, is lost when the absorbed particles meet the singularity. This is the paradox. A static black-hole is uniquely determined by its mass, angular momentum and net electric charge — what is called as the no-hair theorem. All other information is irrelevant to the behavior of a black hole. Now, consider two entangled particles in the event horizon of a black hole. One gets absorbed into the black hole, and the other emitted through the Hawking radiation. The emitted radiation can have no information of the original particle, according to the no-hair theorem. Thus, according to Hawking, the emitted radiation from the black-hole seems to have no information about the initial state. This is unlike how thermal black-body radiation typically tells us about the constituents of the emitting body.
Put differently, the evolution of the quantum wavefunction of these two initially entangled particles, has a component that vanishes irreversibly within the black-hole. Many initial states of the wavefunction result in the same final state, because of ‘no-hair’. This breaks the irreversibility of evolution of the wavefunction in question. i.e., Hawking radiation did not seem to preserve quantum information. This was the paradox.
One of the solutions to the paradox was provided by the Holographic principle which tells that surface area of event horizon increases instead of volume. Information about consumed matter is encoded on the surface area. They say small ridges are formed on the event horizon. You can check out my article on holographic principle and AdS/CFT duality here:
Thank you so much for reading. If you liked this article, you can subscribe for the membership to be a part of my physics community where I share multiple resources, articles and journals of Physics and Mathematics:
Subscribe Now!
Subscribe here to get my articles directly to your email inboxes.
WRITTEN BY
Facts, photos, and articles from and about the history of physics. Twitter @PhysInhistory. Email: physinhistory@gmail.com. www.physhistory.com



0 Comments:
Post a Comment
<< Home